Pressure and temperature of the atmosphere obtained from the gases that make up it.

 

Author; Rogelio Pérez C

Summary;

There is a global problem known as climate change, which consists of an increase in the temperature of the atmosphere, the main focus on this problem is a theory known as the greenhouse effect, This greenhouse effect is attributed almost 33°C of average temperature on the planet. The main greenhouse gases are CO2 and methane, which are also the ones with the least volume in the atmosphere, which is contrary to all known science for the temperature of a gas. As the problem is the increase in the temperature of the atmosphere, and this is a gas, i will use the laws of the gases to present the contributions of the temperature and pressure for each of the main gases that make up the atmosphere in dry air.

Introduction

There is a global problem known as climate change, which consists in the increase of temperature of the atmosphere, the science understands this problem from the hypothesis of a greenhouse effect caused by certain gases; This greenhouse effect is attributed almost 33oC of average temperature on the planet. The main greenhouse gases being CO2 and methane, but as the atmosphere is a gas, the explanation of its temperature can be obtained with charles Law for gases, this  relate the temperature of a gas to its volume, the theory says; For any gas the ratio of temperature to volume are directly proportional, but there are other laws of gases, boyle's law relates the pressure of a gas to its volume, Lussac's gay law governs the relationship between the pressure of a gas and its temperature, and these combined laws put the three together temperature,, pressure and volume of gases, but as the amount of gas must be constant, Avogadro's law relates the volume and quantity of a gas, in moles. And when we combine the 4 laws we get the ideal law of gases, with this law I will explain the temperature and pressure that contribute for each of the gases that make up the atmosphere, in dry air.

Theory;

The Greenhouse Effect. If the earth only absorbed radiation from the sun without giving an equal amount of heat back to space by some means, the planet would continue to warm up until the oceans boiled. We know the oceans are not boiling, and surface thermometers plus satellites have shown that the earth's temperature remains roughly constant from year to year (the interannual globally-averaged variability of about 0.2 C or the 0.5 C warming trend in the 20th century, notwithstanding). This near constancy requires that about as much radiant energy leaves the planet each year in some form as is coming in. In other words, a near-equilibrium or energy balance has been established. The components of this energy balance are crucial to the climate.

All bodies with temperature give off radiant energy. The earth gives off a total amount of radiant energy equivalent to that of a black body -- a fictional structure that represents an ideal radiator -- with a temperature of roughly -18 C (255 K). The mean global surface air temperature is about 14 C (287 K), some 32 C warmer than the earth's black body temperature. The difference is due to the well-established greenhouse effect. U.S. Standard Atmosphere. [1]

Charles' Law

Relationship between the temperature and volume of a gas when the pressure is constant;

In 1787, Jack Charles first studied the relationship between the volume and temperature of a gas sample at constant pressure and observed that when the temperature was increased, the volume of the gas also increased and that when the volume cooled it decreased. [2]

The mathematical expression of this law is:

  VT=k

Boyle's Law

The relationship between the pressure and volume of a gas when the temperature is constant was discovered by Robert Boyle in 1662. Edme Mariotte also reached the same conclusion as Boyle, but did not publish his works until 1676. This is why in many books we find this law called the Law of Boyle and Mariotte.

Boyle's law states that the pressure of a gas in a closed container is inversely proportional to the volume of the container, when the temperature is constant. [3]

The mathematical expression of this law is:

P⋅V=k

Gay-Lussac's law

The relationship between the pressure and the temperature of a gas when the volume is constant was stated by Joseph Louis Gay-Lussac in early 1800. Sets the relationship between the temperature and pressure of a gas when the volume is constant, Gay-Lussac found that at any time during this process, the pressure-temperature ratio always had the same value: [4]

PT=kPT=k

Law of Avogadro

Relation between the amount of gas and its volume

This law, discovered by Avogadro in the early nineteenth century, establishes the relationship between the amount of gas and its volume when temperature and pressure are kept constant. Remember that the amount of gas we measure in moles. [5]

We can also express the law of Avogadro like this:

Vn=k

The ideal gas law, also called the general gas equation, is the equation of state of a ideal gas. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: [6]

PV=nRT

Where P, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It is the same for all gases. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856[7] and Rudolf Clausius in 1857.[8]

The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropriate SI unit is the kelvin. .[9]

Common forms

The most frequently introduced forms are:

PV=nRT=nkBNAT

Where:

P is the pressure of the gas,

V is the volume of the gas,

n is the amount of substance of gas (also known as number of moles),

R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,

KB is the Boltzmann constant

 NA is the Avogadro constant

T is the absolute temperature of the gas.

In SI units, p is measured in pascals, V is measured in cubic metres, n is measured in moles, and T in kelvins (the Kelvin scale is a shifted Celsius scale, where 0.00 K = −273.15 °C, the lowest possible temperature). R has the value 8.314 J/(K·mol) ≈ 2 cal/(K·mol), or 0.0821 l·atm/(mol·K).

Molar form

How much gas is present could be specified by giving the mass instead of the chemical amount of gas. Therefore, an alternative form of the ideal gas law may be useful. The chemical amount (n) (in moles) is equal to total mass of the gas (m) (in kilograms) divided by the molar mass (M) (in kilograms per mole): [10]

n=m/M

By replacing n with m/M and subsequently introducing density ρ = m/V, we get:

PV =m/M.RT

P=m/V.RT/M

P=p. R/M.T

Defining the specific gas constant Rspecific(r) as the ratio R/M,

P=p.R specific.T

This form of the ideal gas law is very useful because it links pressure, density, and temperature in a unique formula independent of the quantity of the considered gas. Alternatively, the law may be written in terms of the specific volume v, the reciprocal of density, as Pv=R.specific.T.

 

Calculating molar mass, density, pressure and temperature in the atmosphere in dry air;

GAS	No. of Moles in 1 Mole Air	Molecular Weight	Mass/grams
Nitrogen (N2)	0,78084	28	21,86352
Oxygen (02)	0,20951	32	6,70432
Argon (Ar)	0,00934	40	0,3736
CO2	0,000415	44	0,01826
Neon (NE)	0,00001818	20.17	0,000366691
Helium (HE)	0,00000524	4	0,00002096
Methane(CH4)	0,00000187	16.04	2,99948E-05
Total weight in 1 mole of air			28,96011765

                  

                           

Density p=M/V                    

Mass with all gases=28960117645 Gram/mole/1000=0, 028960118 Kg/mole        

V=23,6448 L/mole/1000=0,0236448 M³

p=0, 028960118 Kg/mole /0,0236448 M³

p=1,224798588kg/M³

                 

Calculating atmospheric pressure            

PV =m/M.RT                        

P=m/V.RT/M                        

P=p. R/M.T                          

p= Density = 1,224798588kg/M³         

R. specific = 8.31432 J/(mole⋅K)

M= 0,028960118        Kg/mol      

T= Atmosphere temperature.288k o 15°C.

Then                  

P=p. R/M.T                          

P=1,224798588 kg/M³ * 8,314 J/(mole⋅K)/ 0,028960118 Kg/mole *288k

P=1,224798588 kg/M³         287,0844691 J/(mole⋅K) Kg/mole         288k

P= pressure      101266, 7479 Jm³     

 

Calculating atmosphere temperature                          

P=p.R/M.T                           

p.R/M.T=P                  

T=P/p.R/M                     

P= pressure       101266, 7479Jm³      

p=Density 1,224798588kg/M³    

R. specific = 8.31432 J/(mole⋅K)

Mass with all gases= 0,028960118Kg/mole       

T=P/p.R/M                     

T=101266, 7479Jm³ /1,224798588 kg/M³ *  8,314 J/(mole⋅K) /0,028960118 Kg/mole

T=101266, 7479Jm³ /10,18297546 kg/M³/J/(mole⋅K)*0,028960118 Kg/mole

T=101266, 7479Jm³ / 351,6206523M³Jk              

T= Atmosphere temperature.288k or 15°C

Calculating molar mass, density, pressure and temperature in the atmosphere in dry air, without carbon dioxide and methane gases;

GAS	No. of Moles in 1 Mole Air	Molecular Weight	Mass/grams
Nitrogen (N2)	0,78084	28	21,86352
Oxygen (02)	0,20951	32	6,70432
Argon (Ar)	0,00934	40	0,3736
CO2
Neon (NE)	0,00001818	20.17	0,000366691
Helium (HE)	0,00000524	4	0,00002096
Methane(CH4)
Total weight in 1 mole of air			28,94182765

                           

Density                       

p=M/V                         

Mass without GHG=28,94182765 Gram/mol=0,028941828 Kg/mol      

V=23,6448 L/mol=0,0236448M³

p=0.028941828 Kg/mol /0,0236448M³

p=1,224025056 kg/M³         

                           

Calculating atmospheric pressure            

PV =m/M.RT                        

P=m/V.RT/M                        

P=p. R/M.T                          

p= Density = 1,224025 kg/m³.                       

R. specific = 8.31432 J/(mole⋅K)

Mass with all gases= 0, 02896011       Kg/mol      

T= Atmosphere temperature.288k o 15°C.  

Then;                 

P=p. R/M.T                          

P=1,224025056 kg/M³ * 8,314 J/(mole⋅K) /    0,02896011 Kg/mole *288k

P=1,224025056 kg/M³ *287,0844691 J/(mole⋅K) Kg/mole *288k    

P= pressure without GHG = 101202,792 Jm³    

Pressure with all gases = 101266, 7479 Jm³

Difference= 63,92911032 Jm³

Calculating atmosphere temperature                          

P=p.R/M.T                           

p.R/M.T=P                  

T=P/p.R/M                           

P= pressure      101202,792       jm³   

p=Density          1,224025056     kg/M³        

R. specific = 8.31432 J/(mole⋅K). 8,314         J/(mole⋅K).

Mass without GHG= 0,028941828Kg/mole

T=P/p.R/M                           

T=101202,792 jm³      1,224025056 kg/M³    8,314 J/(mole⋅K).        /0,028941828 Kg/mole    

T=101202,792 jm³ /    10,17654432 kg/M³ J/(mole⋅K)./0,028941828 Kg/mole

T=101202,792 jm³      351,6206523m³j/k               

T= Atmosphere temperature without GHG=287,8181 k   

Temperature with all gases=288k or 15°C

Difference= 0,181812729k.

 

Calculating molar mass, density, pressure and temperature in the atmosphere in dry air, without Nitrogen (N2);

GAS	No. of Moles in 1 Mole Air	Molecular Weight	Mass/grams
Nitrogen (N2)
Oxygen (02)	0,20951	32	6,70432
Argon (Ar)	0,00934	40	0,3736
CO2	0,000415	44	0,01826
Neon (NE)	0,00001818	20.17	0,000366691
Helium (HE)	0,00000524	4	0,00002096
Methane(CH4)	0,00000187	16.04	2,99948E-05
Total weight in 1 mole of air			7,096597645

        

Density                       

p=M/V                         

Mass without N2=7, 096597645 Gram/mole=0,007096598 Kg/mole      

V=23,6448 L/mol=0,0236448M³ 

p=0.007096598kg/mole /0.0236448m³

p=0, 300133545 kg/M³  

         Calculating atmospheric pressure without N2           

PV =m/M.RT                        

P=m/V.RT/M                        

P=p. R/M.T                          

p= Density = 0, 300133545 kg/M³                                    

R. specific = 8.31432 J/(mole⋅K)

Mass with all gases= 0, 02896011 Kg/mol 

T= Atmosphere temperature.288k o 15°C.  

Then;                 

P=p. R/M.T                          

P=0,300133545 kg/M³ * 8,314 J/(mole⋅K) /   0,02896011 Kg/mole *288k

P=0,300133545 kg/M³ *287,0844691 J/(mole⋅K) Kg/mole *288k    

P= pressure without N2=24815, 14623 Jm³       

Pressure with all gases =101266, 7479 Jm³

Difference         = 76451,60164 Jm³

Calculating atmosphere temperature        without N2                 

P=p.R/M.T                           

p.R/M.T=P                  

T=P/p.R/M                           

P pressure= 24815, 14623 Jm³ 

p Density= 0, 300133545 kg/M³ 

R. specific = 8.31432 J/(mole⋅K)

Mass without N2 =0,007096598Kg/mole   

 

T=P/p.R/M                           

T=24815, 14623 Jm³ /0, 300133545 kg/M³   *8,314 J/(mole⋅K).       /0,007096598 Kg/mole

T=24815,14623 Jm³ /2,495310293 kg/M³ J/(mole⋅K)./ 0,007096598 Kg/mole

T=24815, 14623 Jm³ / 351,6206523m³j/k              

T= Atmosphere temperature without N2=70,57363k        

Temperature with all gases=288k or 15°C

Difference         = 217, 4263688 k                         

 

Calculating molar mass, density, pressure and temperature in the atmosphere in dry air, without Oxygen (O2);

GAS	No. of Moles in 1 Mole Air	Molecular Weight	Mass/grams
Nitrogen (N2)	0,78084	28	21,86352
Oxygen (02)
Argon (Ar)	0,00934	40	0,3736
CO2	0,000415	44	0,01826
Neon (NE)	0,00001818	20.17	0,000366691
Helium (HE)	0,00000524	4	0,00002096
Methane(CH4)	0,00000187	16.04	2,99948E-05
Total weight in 1 mole of air			22,25579765

 

Density                       

p=M/V                         

Mass without O2=22,25579765 Grams/mole =0, 022255798 Kg/mol    

V=23,6448 L/mol=0,0236448M³

p=0,022255798 kg/mol / 0,0236448M³        

p=0, 941255483     kg/M³              

         Calculating atmospheric pressure without O2          

PV =m/M.RT                        

P=m/V.RT/M                        

P=p. R/M.T                          

p= Density = 0, 941255483 kg/M³                           

R. specific = 8.31432 J/(mole⋅K)

Mass with all gases= 0, 02896011Kg/mol 

T= Atmosphere temperature.288k o 15°C.  

Then;                 

P=p. R/M.T                          

P= 0, 941255483 kg/M³ * 8,314 J/(mole⋅K) / 0,02896011 Kg/mole *288k

P=0, 941255483 kg/M³ *287,0844691 J/(mole⋅K) Kg/mole *288k   

P= pressure without O2=77823, 33177Jm³        

Pressure with all gases =101266, 7479 Jm³

Difference = 23443, 41609 Jm³

 

Calculating atmosphere temperature        without O2                 

P=p.R/M.T                           

p.R/M.T=P                  

T=P/p.R/M                           

P pressure= 77823, 33177Jm³  

p Density= 0, 941255483 kg/M³ 

R. specific = 8.31432 J/(mole⋅K)

Mass without O2 =0, 022255798 Kg/mole 

T=P/p.R/M                           

T=77823, 33177 Jm³ / 0, 941255483 kg/M³  *8,314 J/(mole⋅K).       /0, 022255798 Kg/mole    

T=77823, 33177 Jm³ / 7,825598086 kg/M³ J/(mole⋅K)./ 0, 022255798 Kg/mole        

T=77823, 33177 Jm³ / 351,6206523m³j/k              

T= Atmosphere temperature without O2=221,3275337k

Temperature with all gases=288k or 15°C

Difference = 66, 6724663 k

 

Calculating molar mass, density, pressure and temperature in the atmosphere in dry air, without Argon (Ar);

GAS	No. of Moles in 1 Mole Air	Molecular Weight	Mass/grams
Nitrogen (N2)	0,78084	28	21,86352
Oxygen (02)	0,20951	32	6,70432
Argon (Ar)
CO2	0,000415	44	0,01826
Neon (NE)	0,00001818	20.17	0,000366691
Helium (HE)	0,00000524	4	0,00002096
Methane(CH4)	0,00000187	16.04	2,99948E-05
Total weight in 1 mole of air			28,58651765

        

Density                       

p=M/V                         

Mass without Ar=28,58651765 Grams/mole =0, 02858651 Kg/mol       

V=23,6448 L/mol=0,0236448M³

p=0, 02858651 kg/mol / 0,0236448M³

p=1,208998073      kg/M³                                          

Calculating atmospheric pressure without O2          

PV =m/M.RT                        

P=m/V.RT/M                        

P=p. R/M.T                          

p= Density = 1,208998073 kg/M³                           

R. specific = 8.31432 J/(mole⋅K)

Mass with all gases= 0, 02858651 Kg/mol

T= Atmosphere temperature.288k o 15°C.  

Then;                 

P=p. R/M.T                          

P= 1,208998073 kg/M³ * 8,314 J/(mole⋅K) /  0,02896011 Kg/mole *288k

P=1,208998073 kg/M³ *287,0844691 J/(mole⋅K) Kg/mole *288k    

P= pressure without Ar= 99960, 38257         Jm³  

Pressure with all gases =101266, 7479 Jm³

Difference = 1306, 3653 Jm³

Calculating atmosphere temperature        without Ar                  

P=p.R/M.T                           

p.R/M.T=P                  

T=P/p.R/M                           

P pressure= 99960, 38257 Jm³ 

p Density= 1,208998073 kg/M³  

R. specific = 8.31432 J/(mole⋅K)

Mass without Ar =0, 02858651 Kg/mole    

T=P/p.R/M                           

T=99960, 38257 Jm³ / 1,208998073 kg/M³   *8,314 J/(mole⋅K).       /0, 02858651 Kg/mole    

T=99960, 38257 Jm³ / 10,05160998 kg/M³ J/(mole⋅K)./ 0, 02858651 Kg/mole

T=99960, 38257 Jm³ / 351,6206523m³j/k              

T= Atmosphere temperature without Ar=284,284731k    

Temperature with all gases=288k or 15°C

Difference = 3,715268973 k      

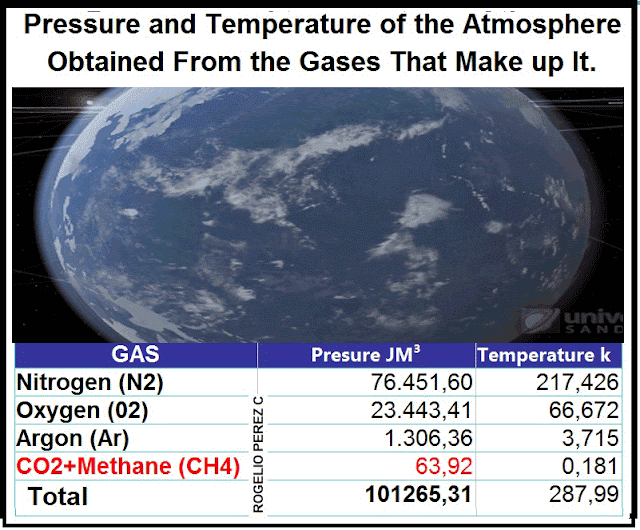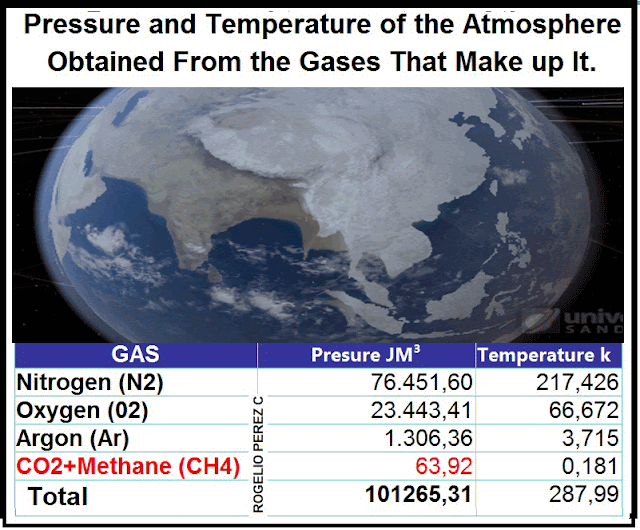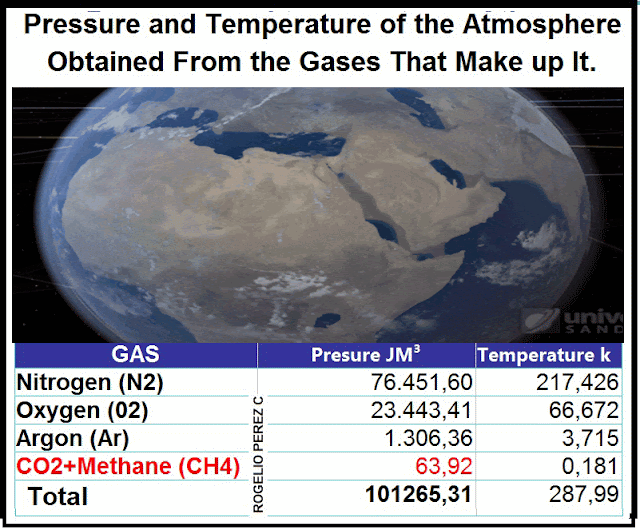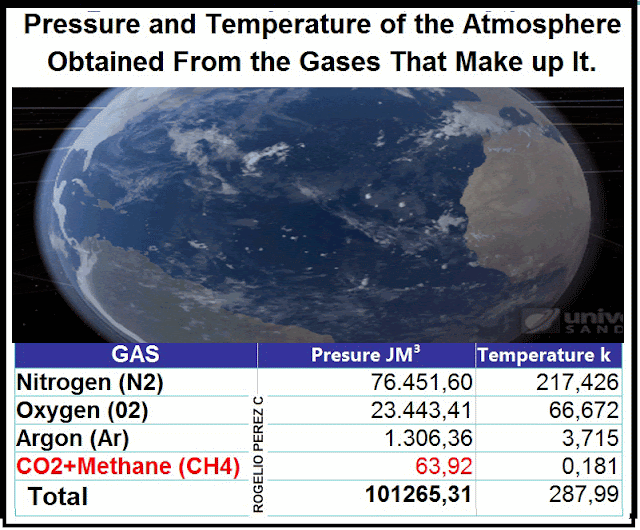
Contribution of each gas that make up the atmosphere in Dry Air, to the pressure and temperature of the planet

GAS	Pressure JM³	Temperature k
Nitrogen (N2)	76451,60164	217,4263688
Oxygen (02)	23443,41609	66,6724663
Argon (Ar)	1306,3653	3,715268973
CO2+Methane (CH4)	63,92911032	0,181812729
Total in  pressure y temperature 1 mole of air	101265,3121	287,995916832

Conclusion,

It can be concluded that if we remove gases such as carbon dioxide and methane from the atmosphere, the temperature of the atmosphere would be almost the same as what we currently have.

It can also be concluded that gases known as greenhouse gases do not contribute at 33°C to the average temperature of the planet.

Finally we can say that the strategy of removing carbon dioxide and methane from the planet's atmosphere is not the best tool for combating heat climates.

Bibliography;

1     https://stephenschneider.stanford.edu/Mediarology/Statement_of_Stephen_Schneider_Climate_Change.html

2-http://www.educaplus.org/gases/ley_charles.html

3-https://www.educaplus.org/gases/ley_boyle.html

4-https://www.educaplus.org/gases/ley_gaylussac.html

5-http://www.educaplus.org/gases/ley_avogadro.html

6-https://en.wikipedia.org/wiki/Ideal_gas_law

7-  Krönig, A. (1856). «Grundzüge einer Theorie der Gase». Annalen der Physik 99 (10): 315-22. Bibcode:1856AnP...175..315K. doi:10.1002/andp.18561751008. (en alemán) Facsimile at the Bibliothèque nationale de France (pp. 315–22).

8- Clausius, R. (1857). «Ueber die Art der Bewegung, welche wir Wärme nennen». Annalen der Physik und Chemie. 3 176: 353-79. Bibcode:1857AnP...176..353C. doi:10.1002/andp.18571760302.

9-Mendeleev, D. I. (1874). «О сжимаемости газов (En la compresibilidad de los gases)». Russian Journal of Chemical Society and the Physical Society 6: 309-352. (en ruso) (From the Laboratory of the University of St. Petersburg).

10- Mendeleev, D. I. (1875). «Об упругости газов (En la compresibilidad de los gases)». Facsimile at the Bibliothèque nationale de France.